Método de Graham

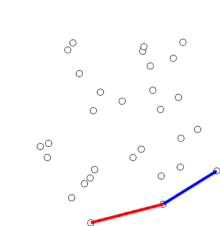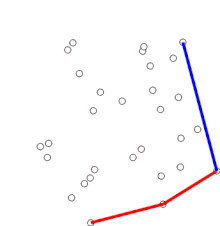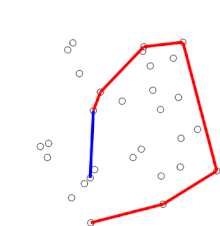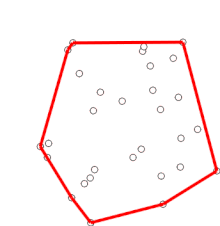
El método de Graham (Graham scan) es un método de cálculo computacional de la envolvente convexa de un conjunto finito de puntos en el plano, de complejidad O(nlogn). El nombre hace honor a Ronald Graham, quien publicó el algoritmo en 1972.^[1] El algoritmo calcula todos los vértices de la envolvente convexa ordenados a lo largo de la frontera. Puede ser fácilmente modificado para calcular los puntos que, sin ser vértices, pertenecen a dicha envolvente.

Algoritmo[editar]

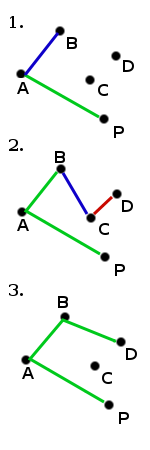
Como se puede ver, el giro entre los vectores PA y AB es contrario a las agujas del rejoj, pero no lo es el giro entre BC y CD. El algoritmo detecta esta situación y descarta los segmentos que llevan a un giro dextrógiro.

El primer paso de este algoritmo consiste en encontrar el punto con la menor coordenada ordenada (menor coordenada en el eje y). Si hay más de un punto que cumpla esta condición, se escoge el punto con menor coordenada en el eje x. A este punto se lo nombra por la letra P. Este paso es de complejidad O(n), donde n es el número de puntos del problema.

Después, el conjunto de puntos debe ser ordenado en orden creciente de ángulo abarcado entre el segmento que los une con el punto P y el eje de abscisas. Para ello se puede utilizar cualquier algoritmo de ordenamiento. Para agilizar el proceso, se puede omitir el cálculo del ángulo ya que es suficiente con hallar su cotangente.

El algoritmo continúa tratando secuencia de puntos ordenados según el ángulo creciente. Para cada punto se calcula si el movimiento desde los dos anteriores es un "giro a derecha" o un "giro a izquierda". Si el movimiento es dextrógiro, indica que el segundo punto de la terna no es parte de la envolvente convexa y debe dejar de considerarse en los cálculos y tomar el siguiente. Cuando se halla un giro a izquierda, el algoritmo pasa a calcular el siguiente punto. En caso de que existan puntos alineados pertenecientes a la envolvente, los centrales pueden ser descartados o considerados como parte de la misma.

No es necesario calcular el ángulo entre tres puntos para saber si es un giro a derecha o a izquierda, pues puede conocerse ese dato con una sola operación aritmética. Para tres puntos $(x_{1},y_{1})$ , $(x_{2},y_{2})$ y $(x_{3},y_{3})$ , se puede calcular el producto vectorial de los dos vectores definidos por las coordenadas $(x_{1},y_{1})$ , $(x_{2},y_{2})$ y $(x_{1},y_{1})$ , $(x_{3},y_{3})$ , de tal manera que el resultado se obtiene con la ecuación $(x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1})$ . Si el resultado es 0, los puntos está alineados, si es positivo, el giro es a izquierdas y, si es negativo, el giro es a derecha.

Finalmente, con este proceso se vuelve al punto P de partida, momento en el que el algoritmo está completado y solo quedan los puntos pertenecientes a la envolvente convexa correctamente ordenados.

Complejidad[editar]

El ordenamiento de los puntos tiene una complejidad O(nlogn). Aunque parezca que la complejidad del proceso es O(n²), pues para cada punto vuelve atrás para comprobar si alguno de las coordenadas anteriores lleva a un giro dextrógiro, realmente es O(n) ya que cada punto se considera como mucho en dos ocasiones en cada sentido. Cada punto puede aparecer solo una vez como $(x_{3},y_{3})$ en un giro a izquierdas ya que el algoritmo avanza al siguiente punto en ese caso y como punto $(x_{2},y_{2})$ en un giro a derechas, ya que en ese caso, el punto es eliminado. La complejidad total es por tanto O(nlogn) ya que el tiempo para ordenar los puntos domina sobre el tiempo necesario para calcular la envolvente.

Notas[editar]

La misma idea básica funciona si los puntos están ordenados según el eje ordenado en lugar del ángulo, y la envolvente se calcula en dos pasos, generando la parte superior y la parte inferior de la misma.

La técnica de apilar datos usada en el método de Graham es muy similar al utilizado en el problema de cálculo del valor menor más cercano, el cual puede ser usado también para calcular eficientemente envolventes convexas de una serie de puntos.^[2]

Referencias[editar]

↑ Graham, R.L. (1972). An Efficient Algorithm for Determining the Convex Hull of a Finite Planar Set. Information Processing Letters 1, 132-133
↑ Berkman, Omer; Schieber, Baruch; Vishkin, Uzi (1993), «Optimal double logarithmic parallel algorithms based on finding all nearest smaller values», Journal of Algorithms 14 (3): 344-370, doi:10.1006/jagm.1993.1018 ..

Datos: Q914780

[1] Graham, R.L. (1972). An Efficient Algorithm for Determining the Convex Hull of a Finite Planar Set. Information Processing Letters 1, 132-133

[2] Berkman, Omer; Schieber, Baruch; Vishkin, Uzi (1993), «Optimal double logarithmic parallel algorithms based on finding all nearest smaller values», Journal of Algorithms 14 (3): 344-370, doi:10.1006/jagm.1993.1018 ..

[1]

[2]